Multiply Using Partial Products Resources
24 results
Math
✕Sort by:
24 results
Sort by:
About Multiply Using Partial Products Resources
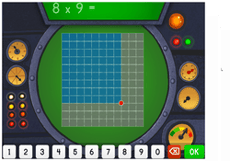
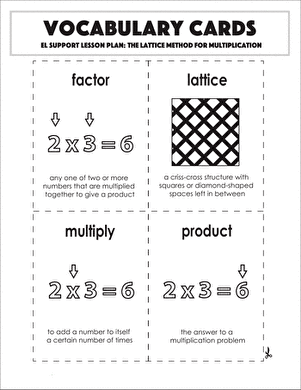
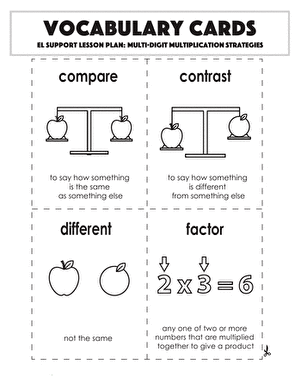
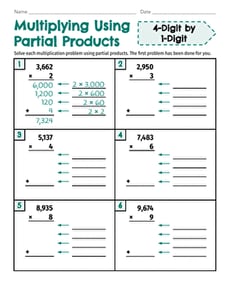
On Education.com, multiply using partial products resources provide tools for teaching and learning the step-by-step process of multiplying multi-digit numbers by breaking the problem into smaller parts. This method helps students understand place value and develop strong multiplication skills. Materials include worksheets, practice problems, and lesson plans that guide students through multiplying tens and ones or wider numbers while emphasizing breaking numbers by place value, multiplying each part, and summing the results.
This page offers worksheets, printable lesson plans, interactive activities, and digital exercises that enable students to practice partial products multiplication in structured and flexible ways. Educators and parents can access resources designed to reinforce place value concepts and build problem-solving strategies. The materials are suitable for classroom or homeschool use and cover foundational to more advanced multiplication applications.
Using these resources at home or in the classroom saves time by providing ready-made, educational materials that support instruction on partial products. Students can practice multiplication step-by-step, gain confidence in handling multi-digit numbers, and strengthen arithmetic fluency. These materials make learning interactive, engaging, and easy to integrate into math practice routines.
This page offers worksheets, printable lesson plans, interactive activities, and digital exercises that enable students to practice partial products multiplication in structured and flexible ways. Educators and parents can access resources designed to reinforce place value concepts and build problem-solving strategies. The materials are suitable for classroom or homeschool use and cover foundational to more advanced multiplication applications.
Using these resources at home or in the classroom saves time by providing ready-made, educational materials that support instruction on partial products. Students can practice multiplication step-by-step, gain confidence in handling multi-digit numbers, and strengthen arithmetic fluency. These materials make learning interactive, engaging, and easy to integrate into math practice routines.